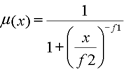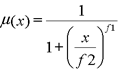تهیه نقشه امکان سنجی آبگرفتگی براساس توابع فازی و AHP در GIS با توجه به فاکتورهای محیطی و شهری

---

در این نوشته ابتدا انواع توابع و فانکشن های عضویت دهی فازی در GIS را به همراه فرمول آنها توضیح دادیم. در مرحله بعد برای یک نمونه روش اعمال این تابع ها روی لایه های مکانی با هدف تعیین پهنه های با پتانسیل بالا را شرح دادیم. با مطالعه این نوشته می آموزید چطور توابع عضویت دهی فازی را برای هر لایه انتخاب کنید و چطور آنها را روی لایه ها با توجه به هدف کار خود اعمال کنید. توابع عضویت دهی و رویهم گذاری لایه های فازی در برنامه GIS برای پهنه بندی یک منطقه مکانی جهت دسته بندی پتانسل های مکانی است.

---

فوری آموز ویدئویی مدل فازی در GIS Pro

---

مهمترین توابع عضویت دهی فازی در GIS عبارتند از:

تابع گوسین (Fuzzy Gaussian Function):

این معادله یا تابع که براساس توزیع نرمال می باشد با مشخص شدن یک نقطه وسط (با عضویت 1) در مجموعه ارزش های نمونه ها (ارزش پیکسل های رستری) ارزش ها در خروجی جدید با یک پراکنش تعریف شده به سمت صفر پخش می شوند و توزیع نرمال پیدا می کنند.  معادله فازی گوسین:

در تمامی معادلات توابع فازی زیر پارامترهای  f1 مقدار پراکنش و f2 ارزش پیکسلی وسط یا نقطه وسط است.  این تابع زمانی کاربرد دارد که عضویت نزدیک یک ارزش ویژه باشد.

معادله فازی بزرگ (Fuzzy Large Function):

تابع بزرگ یا لارج در این رابطه یک تابع عضویت فازی است که ارزش های پیکسلی بالاتر عضویت بیشتر داشته و نزدیک تر به یک هستند. معادله بزرگ:

پارامتر های این معادله همانند قبلی می باشد با این توضیح که ارزش های بیشتری از مقدار پراکنش موجب شیب بیشتر در عضویت فازی می شود.

معادله فازی کوچک (Fuzzy Small Function):

تابع کوچک یا اسمال تابعی است که ارزش های پیکسلی کوچکتر عضویت بیشتری دارند و نزدیک تر به یک هستند.

پارامتر های این معادله نیز همانند قبلی بوده و تغییر ارزشها برعکس معادله بزرگ است.

معادله فازی خطی (Fuzzy Linear Function):

در این تابع عضویت ارزش ها از یک حداقل ارزش پیکسلی تعریف شده بعنوان کمترین عضویت به سمت صفر حداکثر ارزش پیکسلی تعریف شده به عنوان عضویت یک حرکت میکنند.

معادله فازی میانگین انحراف معیار بزرگ (MSLarge):

تابع ام اس لارج تابعی است که براساس میانگین و انحراف معیار ارزش های پیکسلی عمل میکند. در این تابع ارزش های بزرگتر عضویت نزدیک به یک یعنی عضویت بالاتری دارند.

اگر مقدار x بزرگتر از حاصضرب a و m باشد:

u(x) = 1 – (b * s) / (x – (a * m) + (b * s))

که میانگین، انحراف معیار، ضریب میانگین، ضریب انحراف معیار هستند. و اگر مقدار x بزرگتر از حاصضرب a و m باشد:

u(x) = 0

معادله فازی میانگین انحراف معیار کوچک (MSSmall):

در این تابع نیز براساس میانگین و انحراف معیار ارزش های پیکسلی بوده ولی ارزش های کوچکتر عضویت بالاتری دارند و نزدیک تر به یک هستند. در این دومعادله که از ضرایب میانگین انحراف معیار استفاده می شود احتمال اینکه چه مقدار ارزش های بزرگتر عضویت بیشتری یا کمتری در یکی از دو معادله داشته باشند حالت احتمالی است. که ضریب آن میتواند از یک معادله همبستگی بدست بیاید.

معادله نزدیکی فازی (Fuzzy Near Function):

در تابع نزدیکی فازی یک ارزش پیکسلی بعنوان نقطه وسط تعریف می شود که بیشترین عضویت فازی به آن تعلق میگیرد و با یک پراکنش مشخص به اطراف میزان عضویت در بقیه ارزش های پیکسلی کاهش می یابد.

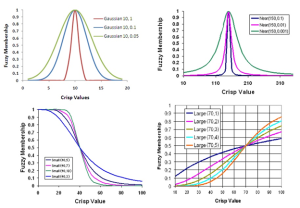
شکل نمودار انواع توابع فازی در GIS

روی هم گذاری یا تلفیق فازی از پنج عملگر عمده استفاده می کند که عبارتند از:

عملگر اشتراک (AND): حداقل عضویت های فازی از بین ارزش های پیکسلی لایه های رستری روی هم گذاری شده در یک نقطه معین انتخاب می شود. عملگر اجتماع (OR): حداکثر عضویت های فازی از بین ارزش های پیکسلی لایه های رستری روی هم گذاری شده در یک نقطه معین انتخاب می شود. عملگر حاصلضرب فازی (PRODUCT): تابع حاصلضرب یک تابع کاهشی است که حاصلضرب ارزش های پیکسلی لایه های مختلف در یک نقطه مشخص را بدست می دهد بطوری که ارزش این حاصلضرب کوچکتر از ارزش پیکسلی هریک از لایه ها در آن نقطه خواهد بود. 

عملگر حاصلجمع فازی (SUM): تابع حاصلضرب یک تابع افزایشی است که حاصلجمع ارزش های پیکسلی لایه های مختلف در یک نقطه مشخص را بدست می دهد بطوری که ارزش این حاصلجمع بزرگتر از ارزش پیکسلی هریک از لایه ها در آن نقطه خواهد بود.  عملگر گامای فازی (GAMMA): این عملگر زمانی است که حاصلضرب دو عملگر قبلی یعنی  حاصلضرب فازی و حاصلجمع فازی به توان ضریب مشخصی از گاما برسد.

در ادامه روش اعمال توابع عضویت دهی فازی روی لایه ها با هدف تعیین پهنه های دارای آبگرفتگی شهری انجام شده است.

در این قسمت روش فازی بر روی چهار لایه اطلاعاتی شیب، فاصله تا فضای سبز، فاصله تا آبراهه ها، و محل های تجمع آب در نرم افزار صص ابتدا عضویت دریافت نموده و سپس روی هم گذاری آنها صورت می گیرد. تمامی این لایه های رستری در مرحله بعد با توابع معین فازی براساس ماهیت و هدف این مطالعه عضویت های متفاوت فازی دریافت می دارند. قبل از اعمال عضویت های فازی برای هر یک از چهار لایه اطلاعاتی، این لایه ها با واحد های مشخص بصورت فایل های رستری آماده سازی شدند.

نتایج اعمال عضویت فازی نشان می دهد که هریک از لایه ها در محدوده های مختلف شهری عضویت های متفاوتی دریافت می دارند. معیارهای چهارگانه هریک تاثیر متفاوتی در آبگرفتگی معابر می توانند داشته باشند. به عبارت دیگر هر معیار ممکن است در آبگرفتگی موثر بوده و یا مانع آن شود. برای این منظور، برای هر یک از معیارها توابع متفاوتی استفاده شده است.

شیب فازی:

از آنجایی که هرچه شیب کمتر باشد احتمال آبگرفتگی بیشتر است. بنابراین طبق تابع کوچک که ارزش های پیکسلی کوچکتر عضویت بیشتری دارند و نزدیک تر به یک هستند، برای دادن عضویت به این لایه از تابع کوچک فازی استفاده شده است.

تجمع آب:

از آنجایی که گودی ها و نقاطی که پست تر هستند و بصورت کانال عمل می کنند احتمال آبگرفتگی بیشتری دارند، برای دادن عضویت به این معیار از تابع فازی میانگین انحراف معیار بزرگ استفاده شده است. چرا که این تابع براساس میانگین و انحراف معیار ارزش های پیکسلی عمل میکند. در این تابع ارزش های بزرگتر عضویت نزدیک به یک یعنی عضویت بالاتری دارند.

فاصله تا فضای سبز:

از آنجایی که فضاهای سبز و پارک ها بانفوذ آب به سفره های زیرزمینی مانع آبگرفتگی می شوند، هرچه نقاط شهری در محدوده شهر کرج به این محل های نزدیک تر باشد احتمال آبگرفتگی آن محل ها کمتر است. بنابراین، از تابع فازی بزرگ برای وزن دادن به این لایه استفاده شده است.

فاصله تا آبراهه ها:

آبراهه ها به عنوان منشا آب ورودی به مناطق شهری، اهمیت زیادی در آبگرفتگی خیابانها  دارند. بنابراین هرچه نقاط به این آبراهه ها نزدیکتر باشند احتمال آبگرفتگی در آنها بیشتر است. به همین منظور از تابع فازی کوچک برای عضویت دادن به این معیار استفاده نموده ایم.

لایه های فازی شده در مرحله بعد با استفاده از تابع گامای فازی رویم هم گذاری می شوند. با روی هم گذاری این لایه ها لایه جدید گامای فازی بدست می آید که پهنه های با احتمال آبگرفتگی متفاوت را در محدود شهری کرج بعنوان منطقه مطالعه این پژوهش نشان می دهد.

روی هم گذاری لایه های فازی شده

نتایج نهایی روی هم گذاری چهار لایه با عضویت فازی محدوده هایی با احتمال آبگرفتگی بالا را نشان می دهد. بنابراین، مشخص شد که قسمت هایی از منطقه 5 و 7 شهرداری کرج بیشترین احتمال آبگرفتگی را نشان می دهد. طبق این نقشه در بخش هایی از منطقه سه و ده نیز در قسمت های جنوبی شهر کرج احتمال آبگرفتگی و ایجاد ترافیک وجود دارد.

وزن دهی به معیارها با AHP

برای وزن دهی به لایه ها و معیارهای مکانیابی یا پهنه بندی می توان از روش های مختلفی استفاده کرد. یکی از روش های بسیار مفید و بسیار قدرتمند در وزندهی به معیار های تصمیم گیری روش AHP یا همان فرایند تحلیل سلسله مراتبی یا فرایند واکاوی سلسله مراتبی است. در این روش معیارها اول بطور زوجی یا یک به یک مقایسه می شوند و سپس وزن های معیار هر کدام نسب به وزن های کل ارزیابی و ورن هر کدام با توجه به هدف مطالعه تعیین می شود. مجموع وزن ها یک است. در ویدئوی فوری آموز زیر می توانید روش استفاده از مدل AHP را در برنامه اکسل (Excel) مشاهده کنید.

در این ویدئو روش استفاده از مدل AHP در نرم افزار اکسل بطور رایگان توضیح داده شده است.

نرم افزار اکسل AHP با روش انتخابی