کاربرد فازی (Fuzzy) در جی ای اس (GIS)

منطق فازی:

ارسطو 300 سال قبل از میلاد منطق دو ارزشی بولین (0و 1) را ارائه کرد که در حال حاضر بنیان و اساس ریاضیات را تشکیل می دهد. این منطق به این موضوع اشاره دارد که یک قانون یا درست است یا درست نیست. برای مثال یک گل رز یا قرمز است یا قرمز نیست، این گل نمی تواند همزمان هم قرمز باشد و هم قرمز نباشد لذا هر عبارت یا جمله ارزشش یا صفر است یا یک. این قانون ارسطو یک قانون فلسفی صحیح است که بیش از 2000 سال مورد استفاده بوده است. اما این منطق همیشه کارایی و کار برد مناسب را ندارد، مثلا برای مثال لیوان نیمه پرآب منطق قدیمی بولین این گونه ابراز می کند که یک لیوان می تواند پر از آب باشد یا نباشد در صورتیکه بسته به نگاه افراد به نیمه پر یا خالی لیوان، را می بینند لذا می توان ابراز داشت که به طور آشکار این موضوع با قانون دو ارزشی ارسطو قابل اثبات نیست. این موضوع چند ارزشی با درجه معین، مفهوم بنیادینی است که دکتر لطفی زاده را در دانشگاه برکلی در دهه 1960 برآن داشت که منطق فازی را معرفی کند [Zadeh,1965]. خصوصیات اساسی منطق فازی ارائه شده بوسیله این محقق به صورت ذیل است:

در منطق فازی هر موضوع یا مفهومی دارای یک درجه عضویت است.
هر سیستم منطقی را می توان به صورت فازی بیان کرد.
در منطق فازی اطلاعات و معلومات به صورت یک مجموعه ای از قیود فازی، معادل یا قیود الاستیک در یک مجموعه ای از متغییر ها بیان می شود.
استنتاج به عنوان یک مرحله ای از انتشار قیود الاستیک بیان می شود.

خصوصیت سوم، از مجموعه خصوصیات ذکر شده توسط زاده منطق بولین را نیز به صورت یک منطق فازی بیان می کند.

فوری آموز ویدئویی آموزش نرم افزاری کاربرد مدل فازی در نرم افزار GIS Pro

فوری آموز ویدئویی مدل فازی در GIS Pro

زوایای کاربرد منطق فازی

سالها اعتقاد بسیاری بر این بود که با پیشرفت علم و دانش عدم قطعیت ها ازبین خواهد رفت. اما در دهه های اخیر وجود عدم قطعیت ها و تناقض ها به صورت اجتناب ناپذیری به عنوان قسمتهایی از سیستم طبیعی پذیرفته شده است. در این زمینه شیوه های قدیمی مواجعه با عدم قطعیت ها از جمله تئوری کاربرد آمار و احتمال در بسیاری از موارد موفق آمیز بوده است، اگرچه کاربرد این تئوریها برای مدلهای پیچیده نیاز به فرضیه های متعدد تئوریکی داشت و عملا به صورت غیرقابل استفاده و بسیار مشکل بوده اند. اکثر اوقات تاکید بیش از اندازه و دقت بسیار سبب پیچیدگی مدلها شده است. حتی در بعضی موارد کاربردآنها عملا امکان پذیر نمی باشد [Bardossy and Duckstein,1995]. اما منطق فازی ابزار دیگر را جهت مقابله با عدم قطعیت ها ارائه می کند، از نظر بسیاری از دانشمندان منطق فازی به عنوان ابزار قابل قبولی در دنیای واقعی علمی بوده که در زمینه های بسیاری کاربرد دارد. به طور کلی مدلهایی که براساس منطق فازی هستند در دو زمینه کاربرد دارند یکی در زمینه های علوم طبیعی (Soft) مشابه علوم اکولوژیکی یا طبی که قوانین پذیرفته شده و دقیقی معمولا برای اهداف مدلینگ وجود ندارد و دیگر در زمینه های علوم سخت (Hard) مانند مهندسی و فیزیک که دارای مدلهای ریاضی پذیرفته شده ای می باشند. مدلهای فازی به راحتی می تواند باهمدیگر پیوند بخورند، برای مثال یک مدل Hard برای جریان در محیط متخلخل ممکن است با یدک مدل رشد باکتری (Soft) همراه شود. علاوه براین، سطح جزئیات مدلها ممکن است تغییر کرده باشد(باتغییر قوانین) بدون اینکه مجبور باشیم مدل را مجددا طراحی کنیم. مدلینگ فازی براساس سیستم های خبره شکل گرفته است . قوانین فازی فقط در همین سیتم های قابل استفاده می شود. این علومن در سیستم های کنترلی در صنایع ژاپن و اروپا به طور ویژه مورد استفاده قرار گرفته اند.

بعضی از علوم (علوم محض و سخت) تلاش می کنند تا رفتار سیستم های فیزیکی را بوسیله یکسری قوانین با استفاده ار سیستم های دینامیکی پیچیده با معادلات دیفرانسیل جزئی بیان کنند. بعنوان مثال مدلهای شناخته شده در دیگر علوم خیلی پیچیده اند . اغلب داده های موجود برای کالیبراسیون و معتبر سازی مدلهای پیچیده کافی نبوده وناهمگنی و یا ناپایداری آنها نیز می تواند باعث انحراف نتایج بدست آمده نسبت به مدلهای تحیلی شود همچنین علومی مانند بیولوژیکی ، اجتماعی، اکولوژیکی، و طبی اطلاعات و دانسته هایشان را در یک شکل مفهومی بیان می کنند تا به صورت یک فرم ریاضی صریح منطق فازی به عنوان یک شکل کلی تری از منطق است که می تواند حقیقت ناقص و ناکامل را به صورت ریاضی درآورده و آنرا محاسبه نماید. پرفسور زاده منطق فازی را به عنوان یک متدولوژی مدلینگ استفاده کرد انتقال ساده تر بین انسان و کامپیوتر را برای تصمیم گیری و روش بهتری را برای محاسبه اطلاعات نادقیق و نامطمئن را ارائه می کرد. این متدولوژی دستخوش توسعه زیادی شده و در حال حاضر به طور گسترده مورد استفاده قرار می گیرد. بعضی از محققین معتقدند که استفاده از منطق فازی باعث افزایش کیفیت و کمیت تکنولوژی های دیگر می شود. مثلا استفاده از این منطق در یک شبکه عصبی برای بیان پارامترهای مورد استفاده به صورت ترمهای فازی باعث افزایش سرعت یادگیری می شود این تنوع کاربری باعث شده که از این منطق بعنوان یک تکنیک اصلی در زمینه های مختلف از جمله علوم محیطی و اکولوزیکی که دارای مدلهای بسیار پیچیده می باشند، استفاده شود.

مدلهای فازی و استنتاج فازی

مدلهای فازی و به طور کلی سیستم استنتاج فازی با توجه به معماری مدل برای به تصویر کشیدن جهان واقعی دارای یک ساختار ثابت با سه قسمت مجزا می باشد. یک مجموعته ورودی تر د که بوسیله توابع عضویت فازی، مجموعه ترد ورودی فازی شده، یک مجموعه قوانین فازی که برای تحلیل ورودی ها ، میزان تاثیر ورودیها بر همدیگر و ارتباط آن با خروجی های سیستم بکار می رود و یک مجموعه خروجی که بااستفاده از روش های دی فازی خروجی سیستم را به یک خروجی ترد تبدیل می کند. برای رسیدن از یک مجموعه ورودی ترد به یک مجموعه یا یک عدد خروجی ترد در مدل فازی ممکن است از عملگرهای مختلف ترکیب گزاره ها و روش های مختلف استدلال و استنتاج فازی و روشهای متفاوت دی فازی براساس فیزیک مسئله مورد بحث استفاده شود که دربخش های بعدی کلیاتی از موضوع مورد استفاده دراین تحقیق ارائه شده است.

تجمیع قوانین فازی

روشهای تجمیع قوانین فازی در دو حالت مجزا قابل بحثند . در روش اول می توان مجموعه ای از قوانین فازی را به عنوان یک قانون فازی، فرض کرد بدین صورت که در ابتدا استلزام های منطقی (R _i)هر قانون را تعین و سپس آنها را ترکیب کرده و انگاه مانند حالت ساده یک قانونیرا براساس رابطه بدست آورده که در آن ترکیب نهایی روابط استلزام بوده که به صورت زیر قابل بیان است:

در معادله فوق نشان دهنده عملگر تجمیع است.

در روش دوم ابتدا نتیجه ترکیب مشاهده را با هر رابطه که قبلا بدست آمده یافته وبیدن طریق بر اساس رابطه بدست می آید، حال نتایج حاصل را با هم تجمیع و استنتاج میشود.

در هر دو روش، انتخاب مناسب برای عملگر تجمیع کننده بستگی به روابط استلزام به کار رفته در و نحوه ارتباط قوانین با یک دیگر دارد. در این تحقیق از روش دوم تجیمع قوانین با ترکیب های برای عملگر تجمیع استفاده شده است.

ترکیب منطق فازی در سیستم اطلاعات جغرافیایی

استفاده از قوانین فازی در سیستم اطلاعات جغرافیایی (GIS) راه را برای اجرای بسیاری از پروژه ها و تحقیقات نرم در علوم طبیعی باز کرده است. با بکارگیری این روش در تحقیقات طبیعی که با عدم قطعیت ها سروکار دارند راه برای رفع بسیاری از مشکلات و پردازش داده های مکانی قابل توجهی باز شده است. در این زمینه مطالعات بسیار زیادی انجام شده است که نتایج آنها بطور موفقیت آمیزی توانسته اند مشکلات و مسایل تعریف شده را حل نمایند و راه کار های مناسب و کاربردی ارایه دهند.

دستورات تجمیع قوانین فازی در GIS شامل مجموعه ای از توابع اشتراک فازی (AND) اجتماع فازی (OR) تجمیع فازی (SUM)، حاصلضرب فازی (PRODUCT)، و گامای فازی (GAMMA) هستند.

مشاهده سایر موارد مورد نیاز شما

عضویت های فازی

عضویت های فازی در GIS (Kevin, 2014) عبارتند از:

معادله اقلیدسی: در این معادله که براساس توزیع نرمال می باشد با مشخص شدن یک نقطه وسط (با عضویت 1) در مجموعه ارزش های نمونه ها (ارزش پیکسل های رستری) ارزش ها در خروجی جدید با یک
پراکنش تعریف شده به سمت صفر حرکت می کنند.
معادله فازی اقلیدسی :

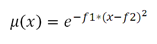
در تمامی معادلات
توابع فازی زیر پارامترهای f1 مقدار پراکنش و f2 ارزش پیکسلی وسط یا نقطه وسط است. این تابع زمانی کاربرد دارد که عضویت نزدیک یک ارزش ویژه باشد.

معادله فازی بزرگ (Large):
این رابطه یک تابع عضویت فازی است که ارزش های پیکسلی بالاتر عضویت بیشتر داشته و نزدیک تر به یک هستند. معادله بزرگ:

Large fuzzy function equation

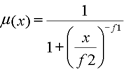
پارامتر های این معادله همانند قبلی می باشد با این توضیح که ارزش های بیشتری از مقدار پراکنش موجب شیب بیشتر در عضویت فازی می شود.

معادله فازی کوچک (Small):
تابعی است که ارزش های پیکسلی کوچکتر عضویت بیشتری دارند و نزدیک تر به یک هستند.

Small fuzzy function equation

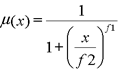
پارامتر های این معادله نیز همانند قبلی بوده و تغییر ارزشها برعکس معادله بزرگ است. همانطور که می بینیم در تابع “کوچک” فقط توان مخرج منفی شده است.

معادله فازی خطی (Linear fuzzy):
در این تابع عضویت ارزش ها از یک حداقل ارزش پیکسلی تعریف شده بعنوان کمترین عضویت به سمت صفر حداکثر ارزش پیکسلی تعریف شده به عنوان عضویت یک حرکت میکنند.

معادله فازی میانگین انحراف معیار بزرگ ( MS Large fuzzy): تابعی است که براساس میانگین و انحراف معیار ارزش های پیکسلی عمل میکند. در این تابع ارزش های بزرگتر عضویت نزدیک به یک یعنی عضویت بالاتری دارند.

(MSLarge)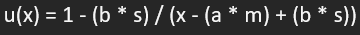

اگر مقدار x بزرگتر از
حاصضرب a
و m باشد:

u(x) = 1
– (b * s) / (x – (a * m) + (b * s))

که میانگین، انحراف معیار، ضریب میانگین، ضریب انحراف معیار هستند. و اگر مقدار x بزرگتر از حاصضرب a و m باشد:

u(x) = 0

معادله فازی میانگین انحراف معیار کوچک (MS Small fuzzy): در این تابع نیز براساس میانگین و انحراف معیار ارزش های پیکسلی بوده ولی ارزش های کوچکتر عضویت بالاتری دارند و نزدیک تر به یک هستند. در این دو معادله که از ضرایب میانگین انحراف معیار استفاده می شود احتمال اینکه چه مقدار ارزش های بزرگتر عضویت بیشتری یا کمتری در یکی از دو معادله داشته باشند. حالت احتمالی است. که ضریب آن میتواند از یک معادله همبستگی بدست بیاید. (MSSmall)

معادله نزدیکی فازی (Near fuzzy): در این تابع یک ارزش پیکسلی بعنوان نقطه وسط تعریف می شود که بیشترین عضویت فازی به آن تعلق میگیرد و با یک پراکنش مشخص به اطراف میزان عضویت در بقیه ارزش های پیکسلی کاهش می یابد. (شکل 4-1)

معادله نزدیکی
فازی:

Near fuzzy function equation

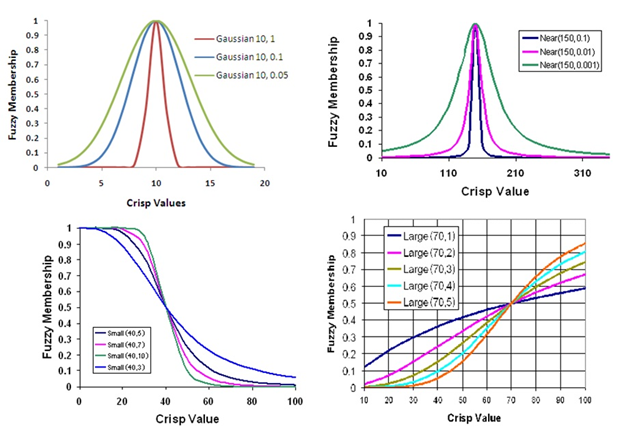
انواع توابع عضویت فازی

روی هم گذاری فازی:

روی هم گذاری یا تلفیق فازی از پنج عملگر عمده استفاده می کند که عبارتند از:

عملگر اشتراک (AND): حداقل عضویت های فازی از بین ارزش های پیکسلی لایه های رستری روی هم گذاری شده در یک نقطه معین انتخاب می شود.

عملگر اجتماع (OR): حداکثر عضویت های فازی از بین ارزش های پیکسلی لایه های رستری روی هم گذاری شده در یک نقطه معین انتخاب می شود.

عملگر حاصلضرب فازی (PRODUCT): تابع حاصلضرب یک تابع کاهشی است که حاصلضرب ارزش های پیکسلی لایه های مختلف در یک نقطه مشخص را بدست می دهد بطوری که ارزش این حاصلضرب کوچکتر از ارزش پیکسلی هریک از لایه ها در آن نقطه خواهد بود.

عملگر حاصلجمع فازی (SUM): تابع حاصلضرب یک تابع افزایشی است که حاصلجمع ارزش های پیکسلی لایه های مختلف در یک نقطه مشخص را بدست می دهد بطوری که ارزش این حاصلجمع بزرگتر از ارزش پیکسلی هریک از لایه ها در آن نقطه خواهد بود. عملگر گامای فازی (GAMMA): این عملگر زمانی است که حاصلضرب دو عملگر قبلی یعنی حاصلضرب فازی و حاصلجمع فازی به توان ضریب مشخصی از گاما برسد.